A Guide About Median Vs. Average What is the Difference?

Median vs. Average

The median of the numbers in a set is the number at which 50% of the numbers are lower, and the other half are higher. The median is the value at which half the homes sold in a given month were lower, while half of them were more expensive.

The average group of numbers is the sum of these numbers multiplied by the number of items within the set. The median and the average could be similar, but they can differ in significant ways; all this relies on the information.

How to Calculate Median and Average

Median

Since it's initially more of the positional average, the set must be laid out in ascending order. Then, the average between the figures at the center is calculated.

Average

It is also the midpoint of the figure set; that's why you add the figures from the group and divide them by the total number of figures included in the collection.

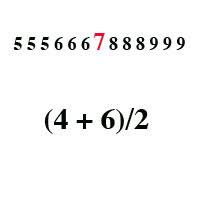
The Key Difference Between the Median And Average

You must be thinking of median vs. average what is the difference? Median and average are used extensively in many areas. They are, however, fundamental tools within the mathematical field and statistics in particular. The median refers to the middle value if the group is set up or ranked according to order.

The median is in the middle of the list. However, to utilize the median, the group members or numbers should be identified or listed in order of rank or sorting. If the list is not populated with members in order of rank, then the numbers need to be written in order of rank. If the member count is not even, select the middle member to be the median.

In contrast, if all members are equal in number and even, it is the average of the two middle numbers. It is thought to constitute the median. However, contrastingly, the average is calculated by summing up all the figures in the group and dividing the increased value by the sum of the participants within the group. It is also called the arithmetic mean.

Usage of Median and Average

Average

The most commonly used kind of average is called the arithmetic mean. It is often utilized in cases where the graph falls within the normal distribution. It is used widely in countries that use numbers to evaluate school performance. However, you can also use it in any scenario where you need to study the data of a set of numbers. The most common use of the average for minimal digits, and only when we have all of the values while making calculations, isn't always the best method to go about it with other types of information.

Median

The most common use of the term "median" is for values that aren't equally dispersed. The idea of an average salary doesn't make sense, but the median pay is a bit more informative. This is the reason why the median is superior. The median eliminates extremes to determine the middle point. This is more important, particularly for vast numbers of values.

The median is sometimes used to indicate the degree to which distribution is oblique in cases where the final values aren't available or when the values outside are not large. For example, if the median is used, it could cause measurement mistakes. Theoretically, the median is a difficult one to deal with.

Why Use The Median Instead of The Average?

The benefit of the median is that it takes away extreme data from a set and gives you a more realistic view of what you can expect. The average can provide more precise information about the full scope of the data. However, when it is about to plan costs and expenses, the median is the most reliable indicator of expectations.

Conclusion

In math, the average and median are distinct. Both can give either the center or average value. Therefore, we must determine its central point, but one is based on statistics, while the other is universally applicable except for classes. Both offer the average value for various stages. We chose the average as a simple value but the median for the range or category. Now you understand the difference between the average and the median in statistics or mathematics. It's crucial to be aware of this distinction to avoid being lost when reading a statistic or article.